Reading Time: 6 minutes

The article guides you to Hashgraph, a patented Distributed Ledger Technology(DLT) in the form of a Directed Acyclic Graph(DAG) and its unique underlying consensus algorithm.

Why I am writing on it, and what brings me to know about Hashgraph?

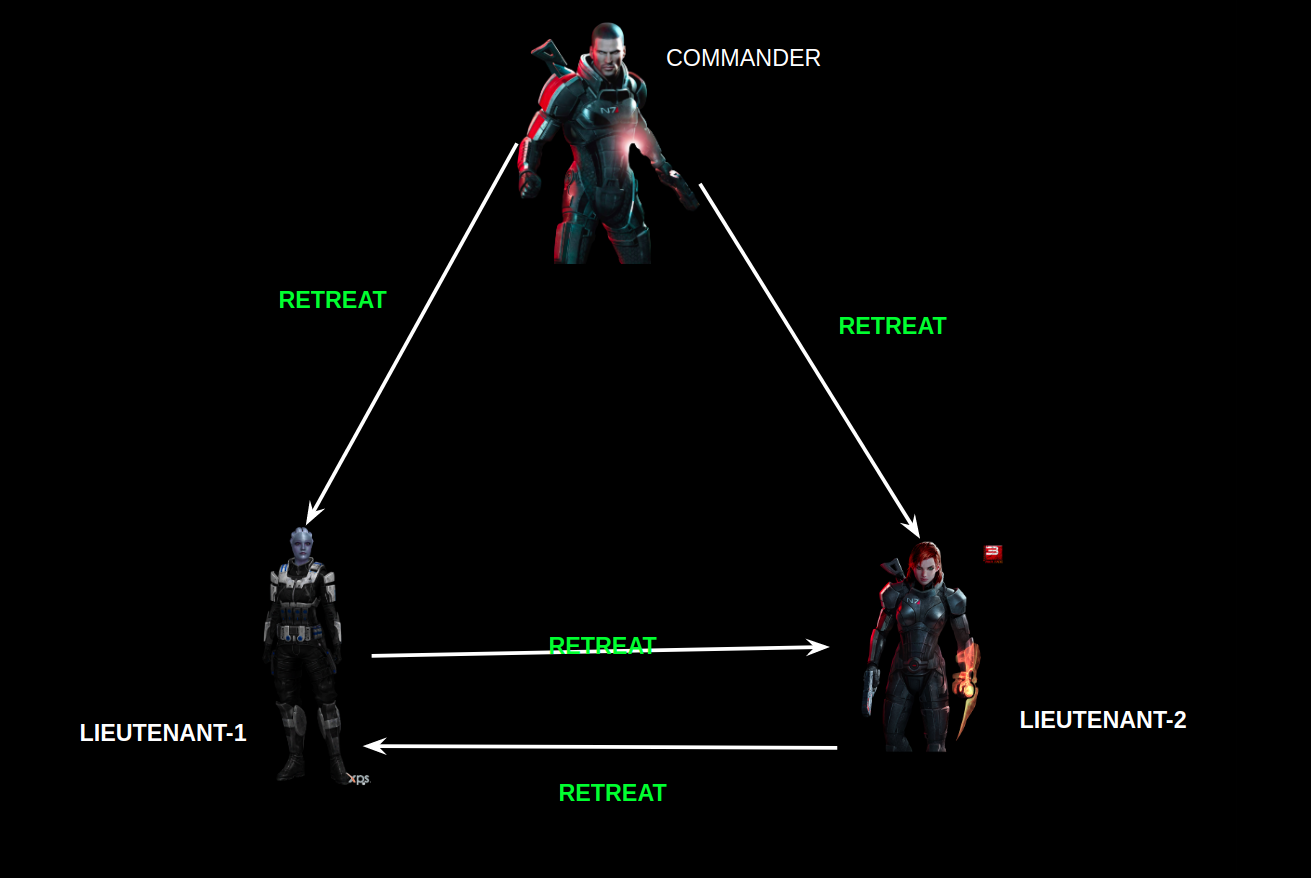
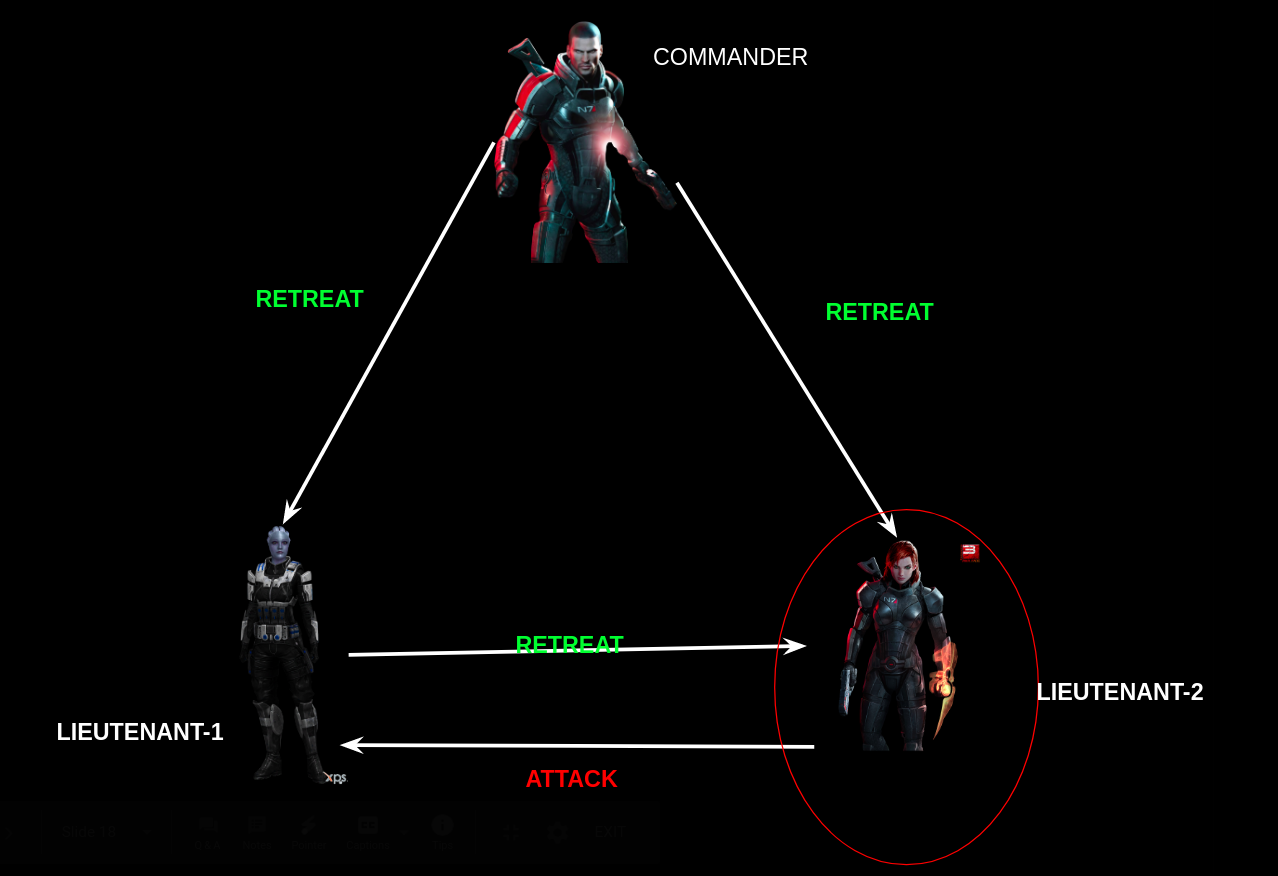
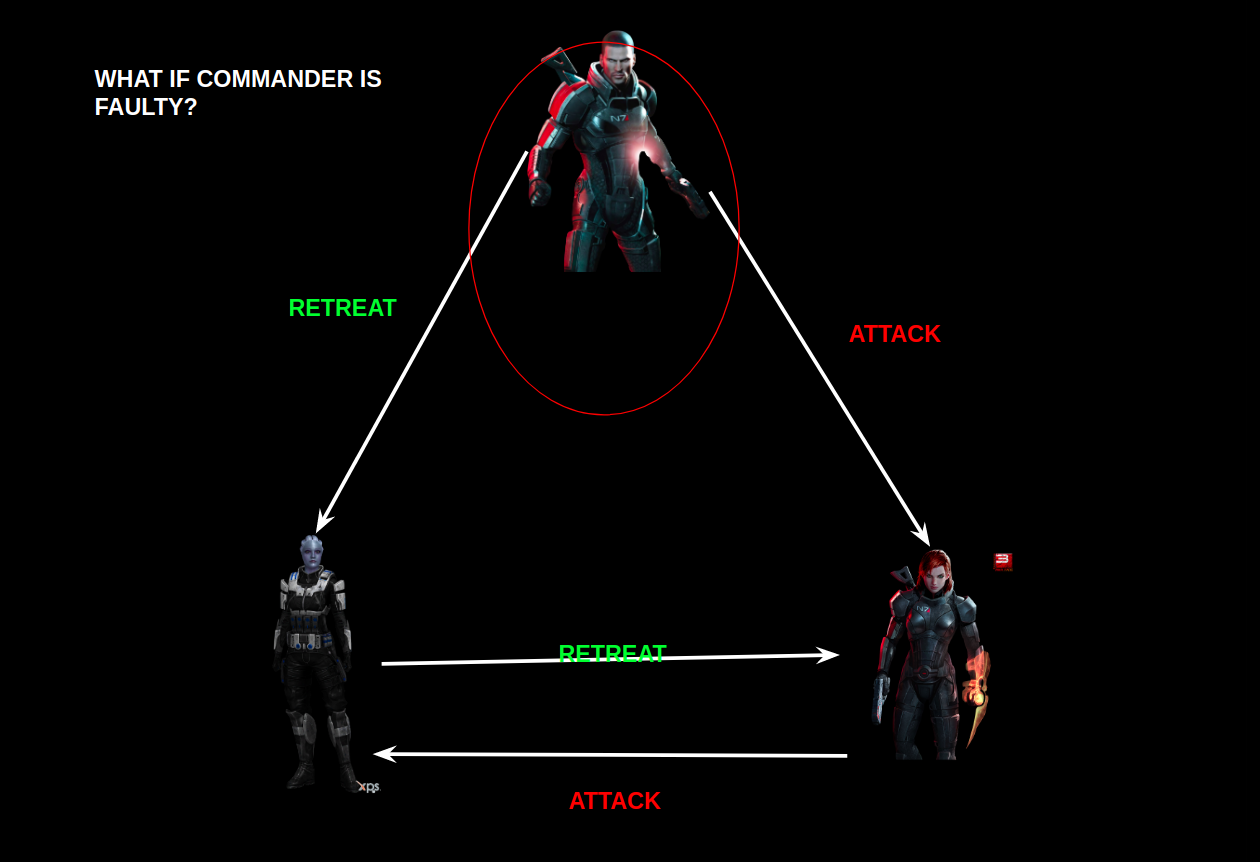
While working on some project, I had been assigned a sub-task to plug in a consensus algorithm to ensure fair ordering of transactions during my intern. The use-case was critical and it was very important to ensure proper ordering of transactions.

You can find, many use-cases, where the fair ordering of transactions is a critical requirement. As an example, consider an online decentralized auction platform. Different users are bidding on something. Say one person bids on a certain value and hearing his value another person bids higher than his value. If the fair ordering of transaction is not ensured then the second person may win the auction, which should not happen.

Similarly, the project in which I was involved, dealt with a fair allocation of computing resources to the requestors along with good throughput and this indeed requires fair ordering of requests(transactions).

After a lot of literature survey and searching for some new ideas, I came across the Hedera Hashgraph project and it solved my problem.

Hashgraph ensures fair ordering of transactions.

Another characteristic or we can say feature because of which ‘Hashgraph’ is getting buzz is its high throughput of transactions and a very short delay in transaction’s confirmation.

Hashgraph ensures high thoughput of transactions.

The scalability problem is common in Blockchain Networks. The bitcoin’s theoretical transaction throughput is 27 transactions/sec. There are always some limitations in various already proposed consensus algorithms which limits the transaction throughput.

Check out this video by Dr Leemon Baird[founder of Hashgraph] explaining the drawbacks of Proof of Work:

Try to watch other videos of the playlist, it explains why different consensus algorithms involving leader election, voting etc can’t achieve a great performance.

So, he (Dr Leemon Baird) came with the idea of hashgraph, which solves much of the issues and ensure fair ordering with high throughput.

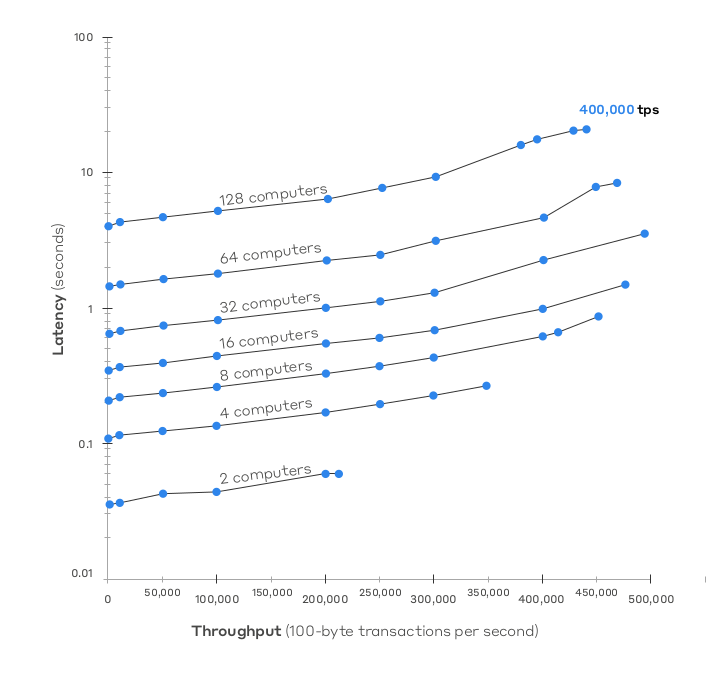
How Hashgraph achieves a better performance?

The reason for good performance the hashgraph, when compared to other DLTs, depends on these ‘Infinity Stones’:

Hashgraph-a directed acyclic graph data structure that records who gossiped to whom, and in what order.
Gossip about Gossip-the hashgraph is spread through the gossip protocol. The information being gossiped is the history of the gossip itself, so it is “gossip about gossip”. This uses very little bandwidth overhead beyond simply gossiping the transactions alone.
Virtual Voting– every member has a copy of the hashgraph, so Alice can
calculate what vote Bob would have sent her if they had been running
a traditional Byzantine agreement protocol that involved sending votes.
So Bob doesn’t need to actually hear the vote.

Check out this video for more clarity on Virtual Voting-

Hashgraph Consensus

The idea to achieve consensus in the hashgraph consensus algorithm is based upon the ‘Gossip’ protocol, which isn’t a new thing. ‘Gossip’ protocols call other participants repeatedly and pass them all the events they don’t know about. The ‘gossip’ method is being used in many traditional message passing algorithms. So what makes ‘Hashgraph’ different? Let’s catch it up.

In hashgraph, rather than normal gossip protocols, the whole hashgraph is gossiped. It is said the information is being communicated through ‘gossip about gossip’.

If one participant doesn’t know about some event, then some other node will gossip the missing information to him. All these events can be represented by a Directed Acyclic Graph(DAG).

If a new transaction is placed in the payload of an event, it will quickly spread to all members, until every member knows it. e.g. Alice will learn of the transaction. And she will know exactly when Bob learned of the transaction. And she will know exactly when Carol learned of the fact that Bob had learned of that transaction.

What’s inside the event?

Consider the case, Alice, Bob, Carol and Dave are members. Bob calls Dave. So Dave creates a new event to record this.

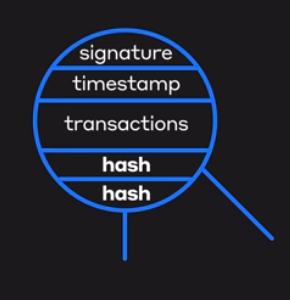
So the new event holds the Signature of Dave and the two hashes of the events prior to sync i.e self-parent(parent directly below) and other-parent(the event though which gossip is being done). Along with this event holds the list of transactions and timestamp which acts as a proof/vote of when did this event occur?

As the time pass, this event keeps passing along with the other events. So the whole network knows, when did this event occur and Dave created this.

It gives rise to an immutable, distributed data-structure which doesn’t contain linear blocks chained together for cryptographic immutability, instead, a directed acyclic graph(DAG).

The hashgraph at every node stores the entire history about ‘who gossip to whom and when’. So without the actual transfer of votes, the consensus algorithm moves toward the concept of virtual-voting for reaching consensus on the ordering of transactions.

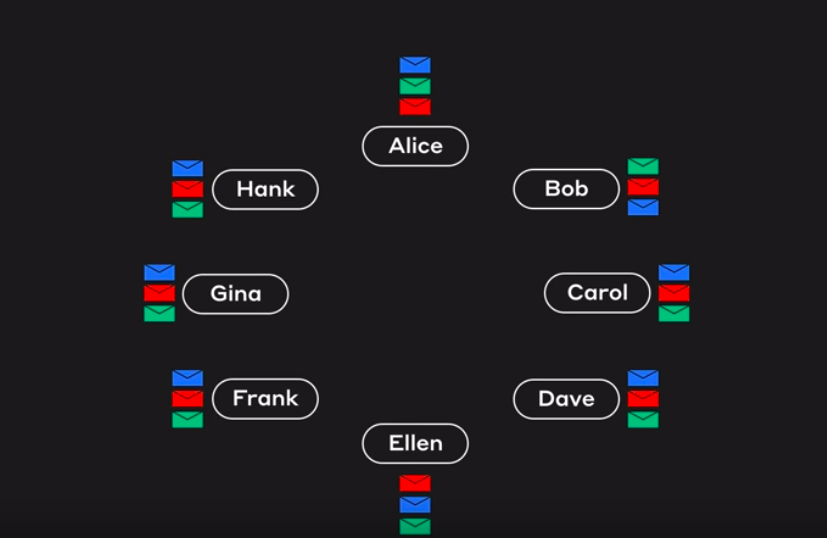
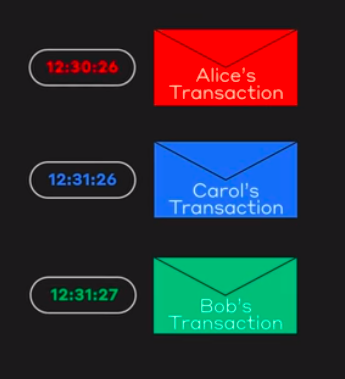
The whole idea for fair-ordering revolves around the fact that each node knows all the event. So when a transaction is spread throughout the network, the hashgraph records the event containing the transaction. So, if we consider a transaction, it would have reached different nodes at different times. We can represent the consensus timestamp of this transaction with mean of all the event timestamps or the median of the event timestamp. Parallelly, if another transaction is spread, then the graph also holds the consensus timestamp of the other transaction indirectly. This consensus timestamp can be used to order the transaction.

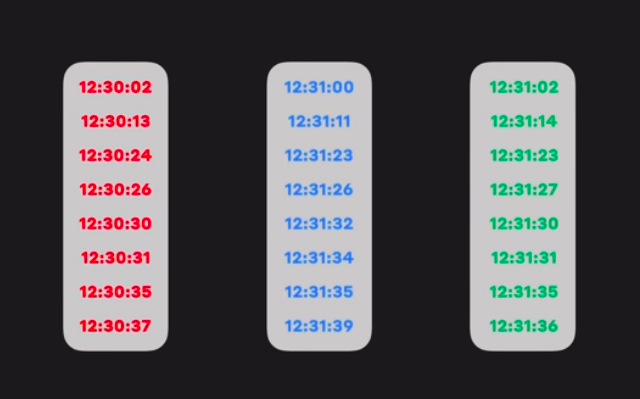
Using these timestamps, the mean or median timestamp is obtained which represents the consensus timestamp and is used for fair ordering.

That’s all if you want to know more about visit hashgraph check out the references.

For more details and mathematical theorems behind the consensus, refer the original paper.

References:

https://www.swirlds.com/downloads/SWIRLDS-TR-2016-01.pdf
https://www.hedera.com/hh-whitepaper-v2.0-17Sep19.pdf
Hashgraph Consensus Algorithm Explained | Dr Leemon Baird-https://www.youtube.com/watch?v=cje1vuVKhwY
Swirds’ Leemon Baird Talks Hashgraph-https://www.youtube.com/watch?v=pOc23lJw7ls
https://www.forbes.com/sites/forbesdigitalassets/2019/09/26/hedera-hashgraph-explored/#58cb3df27bd0

Reading Time: 5 minutes

This short-article focusses on one of the most popular consensus problems in distributed computing known as “Byzantine’s General Problem” and when a distributed system is said to be Byzantine Fault Tolerant.
Various Byzantine Fault Tolerant algorithms are being used in Permissioned Blockchain Networks e.g Hyperledger Sawtooth is using Practical Byzantine Fault Tolerant(PBFT) to achieve consensus. So, if you want to understand how the consensus is actually achieved in such systems. This article is surely for you.

So let’s begin this journey.

First of let’s focus on the term ‘Byzantine Fault Tolerant’ and when a distributed system is said to be Byzantine Fault Tolerant?
The answer lies within the different types of failures that can occur in a distributed system-

1.Crash-Fail: In this type of failure, the component stop working without any warning. So you need to restart the node or replace it. We can say it is a ‘Fail-Stop’ failure.

2.Omission Failure: In this, component transmits a message but that message is not received by other nodes or we can say it is omitted.

3.Byzantine Failures: It is a ‘no-stop failure’.It occurs when there is a malicious or traitor node in the network which sends conflicting messages or block the messages by not sending them to the other nodes in the network, which may lead to faulty results.

Now I think it is self-explanatory that a distributed system is said to be Byzantine Fault Tolerant if it can cope-up with the Byzantine Failures.

The applications of BFT can be found in various domain like Blockchain and even in Boeing 777 and 787 flight controls.

Let’s move on to a specific problem which forms a base for understanding BFT-

The Byzantine General’s Problem :

Situation: Suppose there are several generals and they have to attack army camp C and they are surrounding the army camp such that they can’t communicate with each other directly. The only way communication can happen in between them is through a carrier and he needs to pass the enemy camp for transferring every message.
So they need proper protocols to reach a final decision whether to “attack ” on C, the next morning or “retreat”.
If they all agree to attack, and they do attack then they will surely win or if they agree to “retreat” then they can fight on another day. But if one of the general attack and other decides to retreat then they are surely gonna lose.

Problems:

Malicious Generals create variation in the decision to the others
Message Carriers may not reach
Reach a single solution, considering the downsides of a few Generals

Keeping in mind the situation, let’s discuss this problem with three generals.

Three Generals Problem:

Suppose, there are one commander and two lieutenants surrounding the army camp C and they have to collectively reach a decision to ‘attack’ or ‘retreat’.

If neither of the generals is faulty then all will work good and they will surely reach a decision.