This short-article focusses on one of the most popular consensus problems in distributed computing known as “Byzantine’s General Problem” and when a distributed system is said to be Byzantine Fault Tolerant.
Various Byzantine Fault Tolerant algorithms are being used in Permissioned Blockchain Networks e.g Hyperledger Sawtooth is using Practical Byzantine Fault Tolerant(PBFT) to achieve consensus. So, if you want to understand how the consensus is actually achieved in such systems. This article is surely for you.
So let’s begin this journey.
First of let’s focus on the term ‘Byzantine Fault Tolerant’ and when a distributed system is said to be Byzantine Fault Tolerant?
The answer lies within the different types of failures that can occur in a distributed system-
1.Crash-Fail: In this type of failure, the component stop working without any warning. So you need to restart the node or replace it. We can say it is a ‘Fail-Stop’ failure.
2.Omission Failure: In this, component transmits a message but that message is not received by other nodes or we can say it is omitted.
3.Byzantine Failures: It is a ‘no-stop failure’.It occurs when there is a malicious or traitor node in the network which sends conflicting messages or block the messages by not sending them to the other nodes in the network, which may lead to faulty results.
Now I think it is self-explanatory that a distributed system is said to be Byzantine Fault Tolerant if it can cope-up with the Byzantine Failures.
The applications of BFT can be found in various domain like Blockchain and even in Boeing 777 and 787 flight controls.
Let’s move on to a specific problem which forms a base for understanding BFT-
The Byzantine General’s Problem :
Situation: Suppose there are several generals and they have to attack army camp C and they are surrounding the army camp such that they can’t communicate with each other directly. The only way communication can happen in between them is through a carrier and he needs to pass the enemy camp for transferring every message.
So they need proper protocols to reach a final decision whether to “attack ” on C, the next morning or “retreat”.
If they all agree to attack, and they do attack then they will surely win or if they agree to “retreat” then they can fight on another day. But if one of the general attack and other decides to retreat then they are surely gonna lose.
Problems:
- Malicious Generals create variation in the decision to the others
- Message Carriers may not reach
- Reach a single solution, considering the downsides of a few Generals
Keeping in mind the situation, let’s discuss this problem with three generals.
Three Generals Problem:
Suppose, there are one commander and two lieutenants surrounding the army camp C and they have to collectively reach a decision to ‘attack’ or ‘retreat’.
If neither of the generals is faulty then all will work good and they will surely reach a decision.
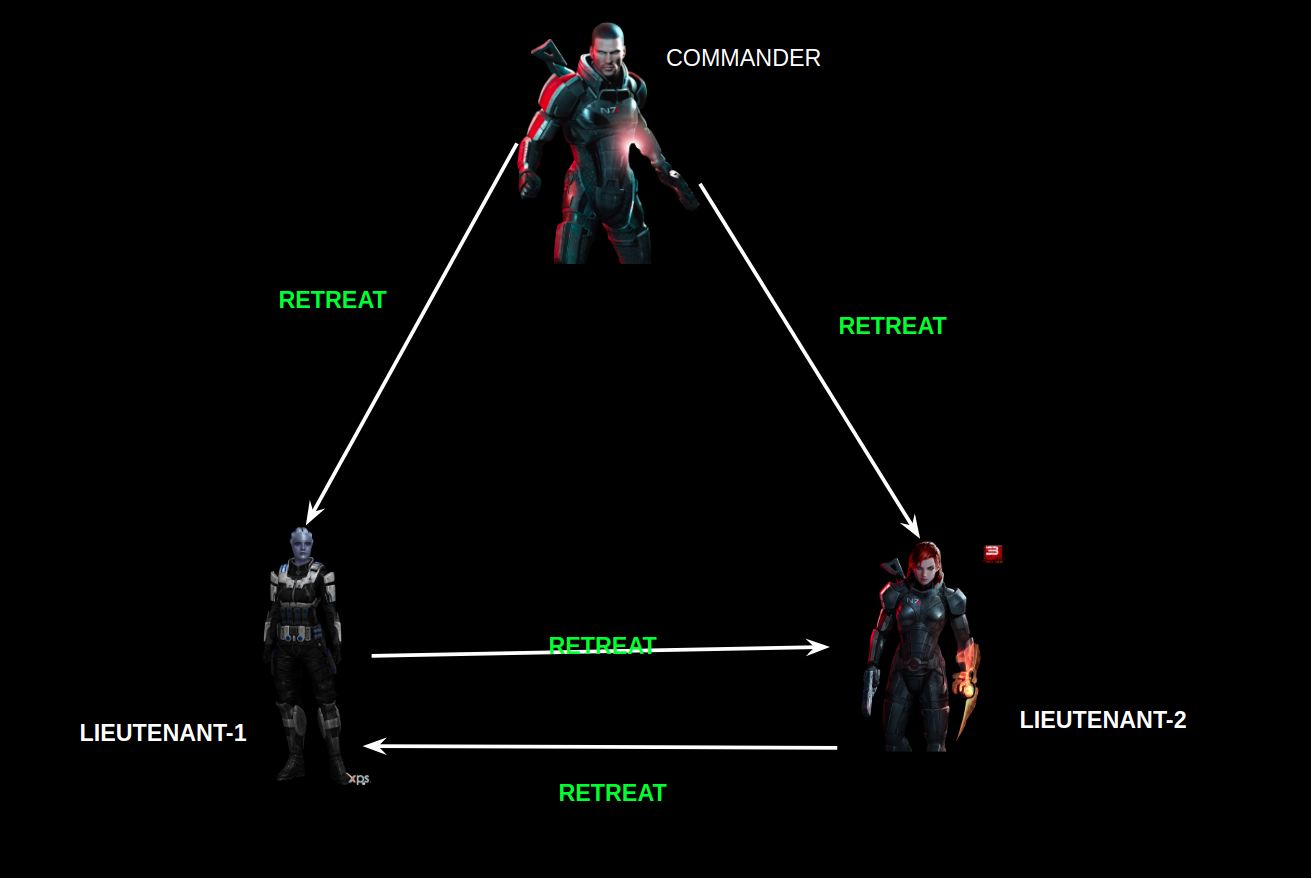
Let’s see the case if one of the generals starts behaving maliciously:
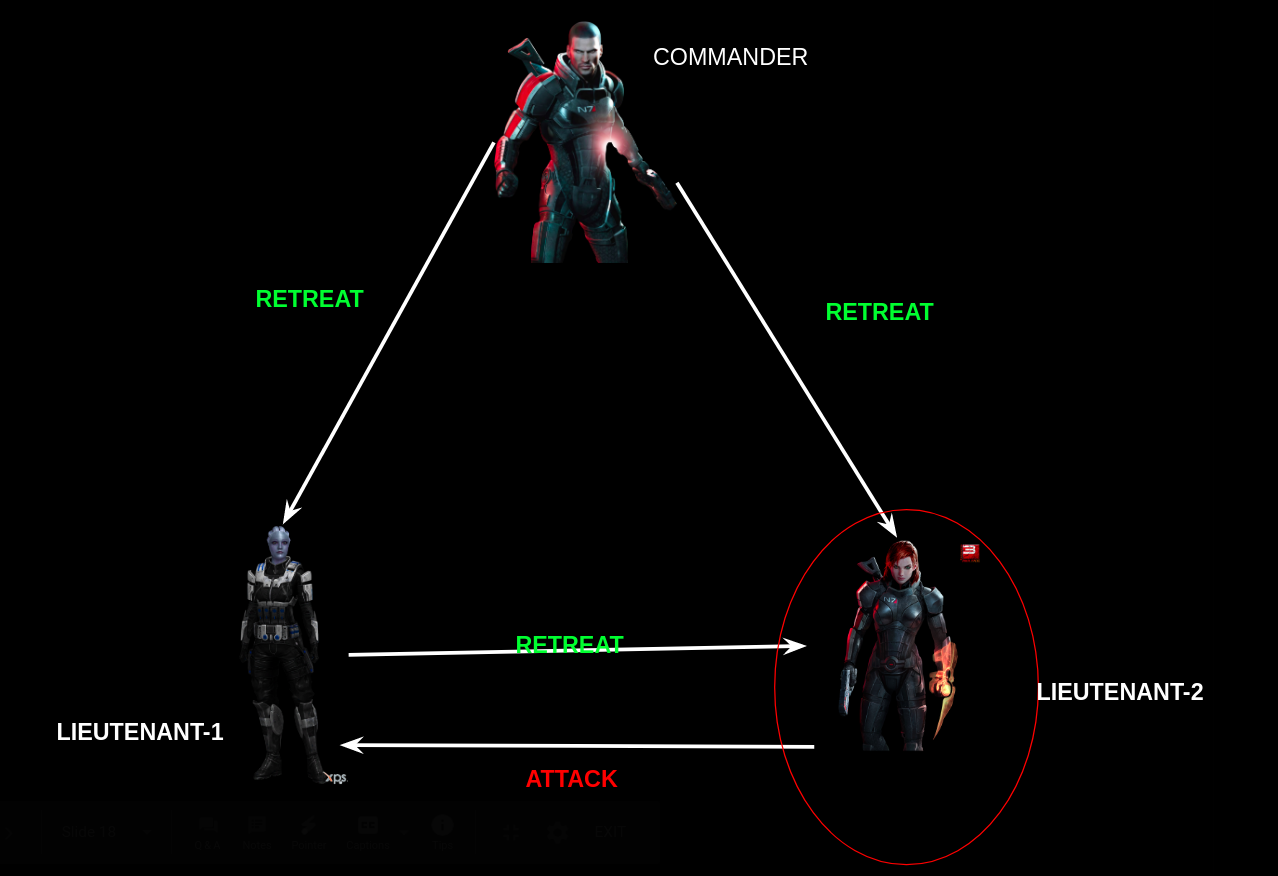
Let’s break up the whole communication process in two phases.
Phase-1: Commander sends the messages correctly to lieutenants.
Phase-2: Lieutenant-1 correctly forwards the message to Lieutenant-2.
As Lieutenant-2 is malicious, so he forwards the message to Lieutenant-1 incorrectly.
Clearly, Lieutenant-1 is receiving differing messages.
Let’s take a look at another possibility before jumping onto the conclusion.
What will be the case if ‘Commander’ is faulty?
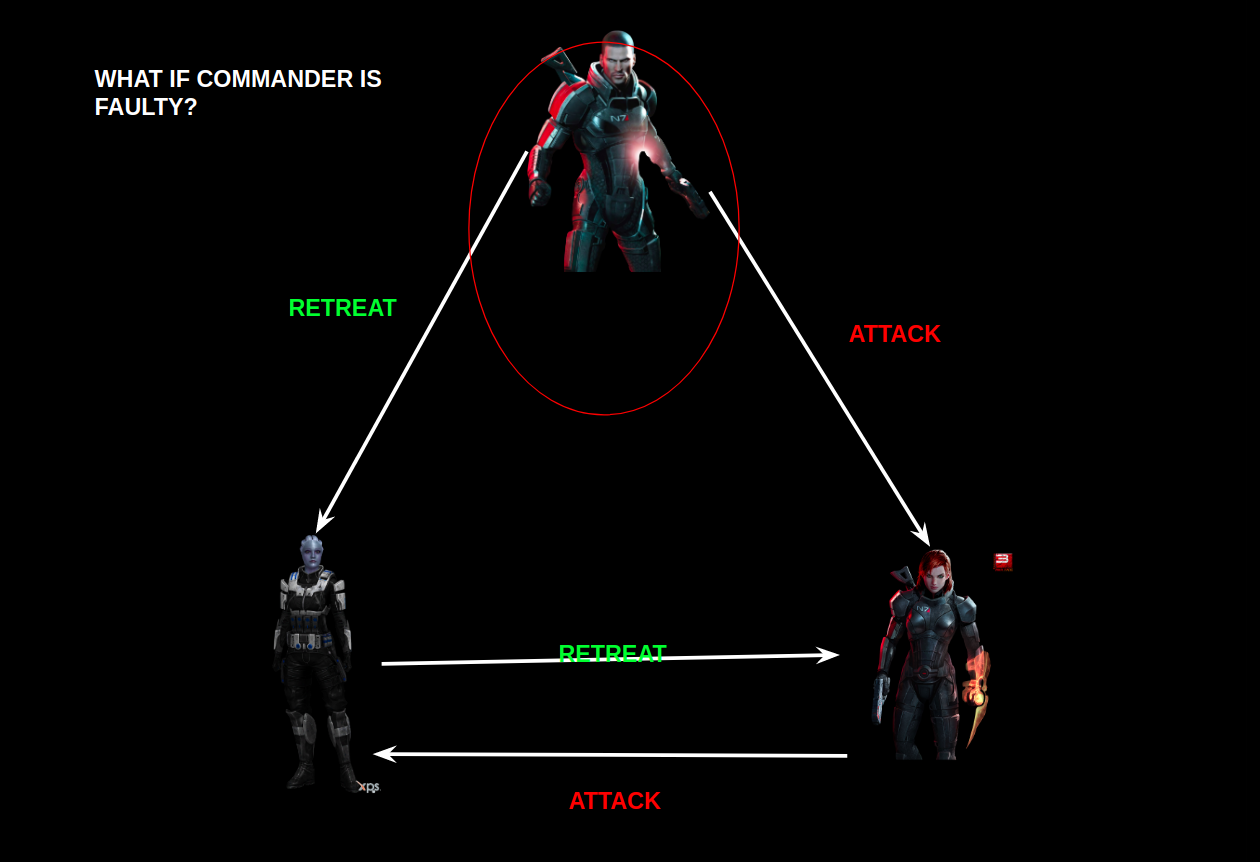
Phase-1: Lieutenant-1 and Lieutenant-2 recieves different messages.
Phase-2: They both exchange the messages correctly as they are loyal.
As per the protocols, both Lieutenants have to follow the Commander’s message. This is in the contradiction of the agreement condition.
Conclusion: There is no solution possible for ‘Three Generals Problem’ if one of the generals is faulty.
Four Generals Problem
Suppose, there are one commander and three lieutenants surrounding the army camp C and they have to collectively reach a decision to ‘attack’ or ‘retreat’.
When one of the Lieutenant is faulty?
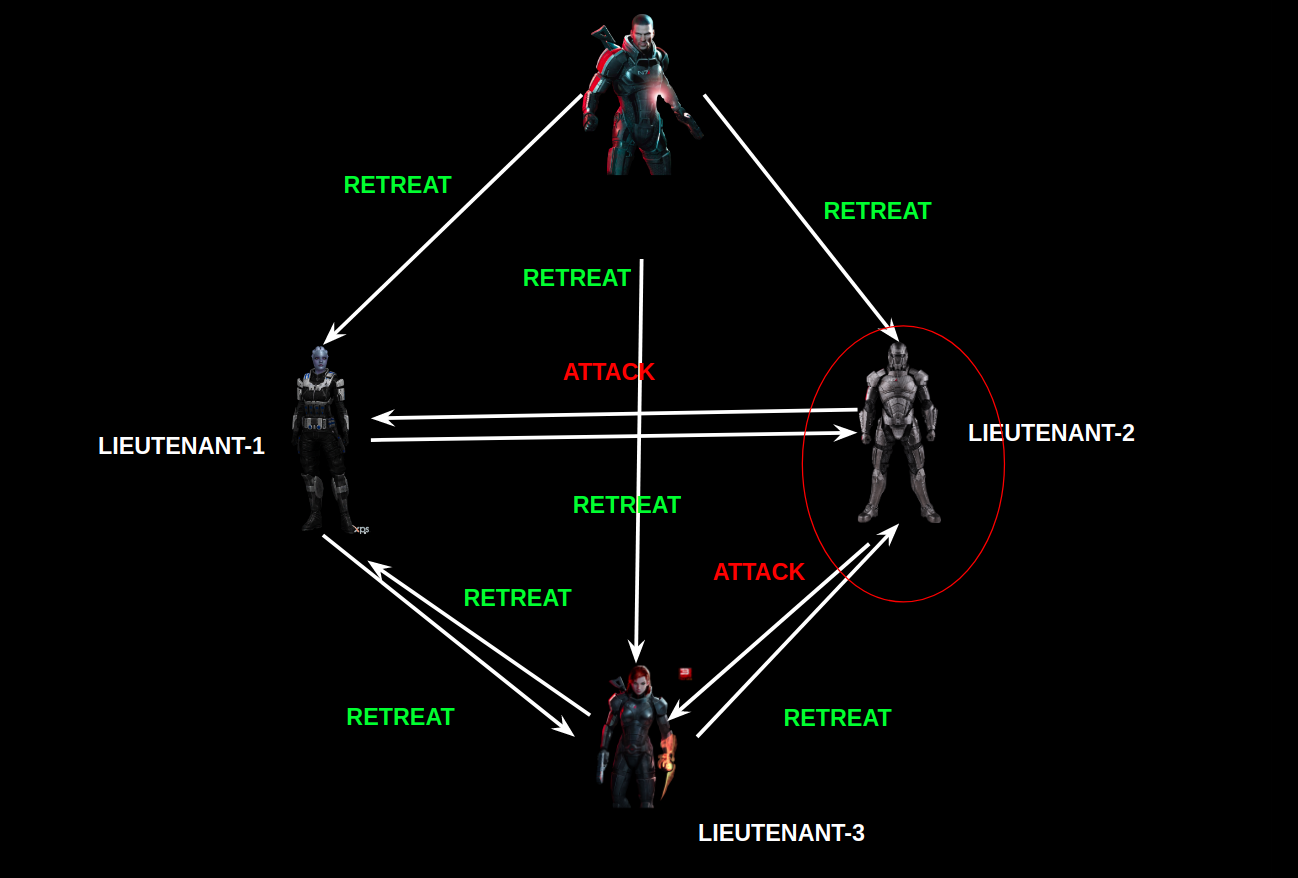
Phase-1: Commander correctly sends the message to other lieutenants.
Phase-2: Lieutenant-1 & Lieutenant-3 correctly forwards the message to others.
Lieutenant-2 behaves in a byzantine manner and incorrectly transmits the message.
By Majority Voting, the non-malicious lieutenants can reach the decision.
Decision of Lieutenant-1:
Majority(Retreat,Attack,Retreat)=Retreat
Decision of Lieutenant-2:
Majority(Retreat,Retreat,Attack)= Retreat
So, they have reached the consensus i.e “To Retreat”.
When the Commander is faulty?

I think you can deduce what will happen in the two phases now.
Jumping directly to the decisions:-
Decision of Lieutenant-1:
Majority(Retreat,Attack,Retreat)=Retreat
Decision of Lieutenant-2:
Majority(Attack,Retreat,Retreat)= Retreat
Decision of Lieutenant-3:
Majority(Retreat,Retreat,Attack)=Retreat
So, the consensus has been achieved with the decision “To Retreat”.
One more special thing to observe here is that the final agreement will be the one which is in the majority of the decisions in Phase-1 e.g Retreat is in majority in Phase-1. So final agreement is on “Retreat‘’.
Conclusion: If out of 4 generals, only one is faulty or behaving in a byzantine way, then we can reach the agreement and consensus is achieved.
By the above two scenarios, we can now generalise the Byzantine Model of Distributed Systems.
Generalization
A System having ‘f’ number of faulty nodes(generals) should have at least, in total 3f+1 nodes(generals) in the network to reach the consensus.
Thanks for showing patience and reading until the end.
Next in the series is ‘PBFT & RBFT Consensus’ and ‘Consensus in Public Blockchain Networks’.
References:
https://people.eecs.berkeley.edu/~luca/cs174/byzantine.pdf