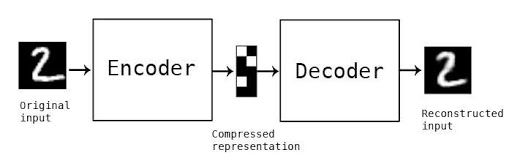
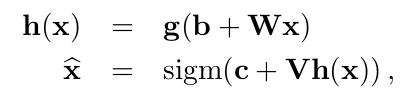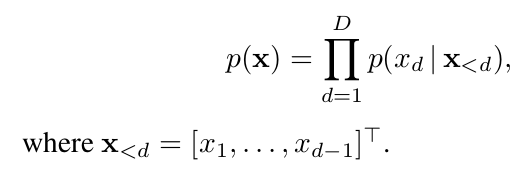With great power comes great responsibility. These are the words of Stan Lee author of the Spider-Man comic book series but where does data power arise from and what are the responsibilities for us as data scientists? First let’s talk about power. In May 2017 the Economist ran the following headline “The world’s most valuable resource is no longer oil but data in fact”. The data as the replacement oil analogy originated from 2006 when Clive Humbly from Tesco in the UK said data is the replacement oil. It’s valuable, but unrefined, it’s useless, and that’s where you come in.
Being a data scientist is a powerful and privileged role; you have highly sought after skills, skills that most people cannot learn. So, you may be granted respect, authority and power simply for being a data scientist. Let’s talk about responsibility. When you think of data science you might think of business models like those that optimize ad revenue. Even these seemingly trivial data science tasks come with a lot of responsibility. A small mistake could lead to a lot of money lost for your company. Data science is used in every field imaginable from marketing to medicine and from transportation to waste management. While a data scientist might feel a bit removed from the real-world implementations of their work their models and analytics will eventually affect real-life decisions. As such, data scientists must adhere to ethical principles when handling data. Data science ethics involves principles, guidelines, and standards that guide data use responsibly and fairly. Data scientists have access to an immense amount of data, and they should use it judiciously and responsibly. The following are some ethical considerations for data scientists.
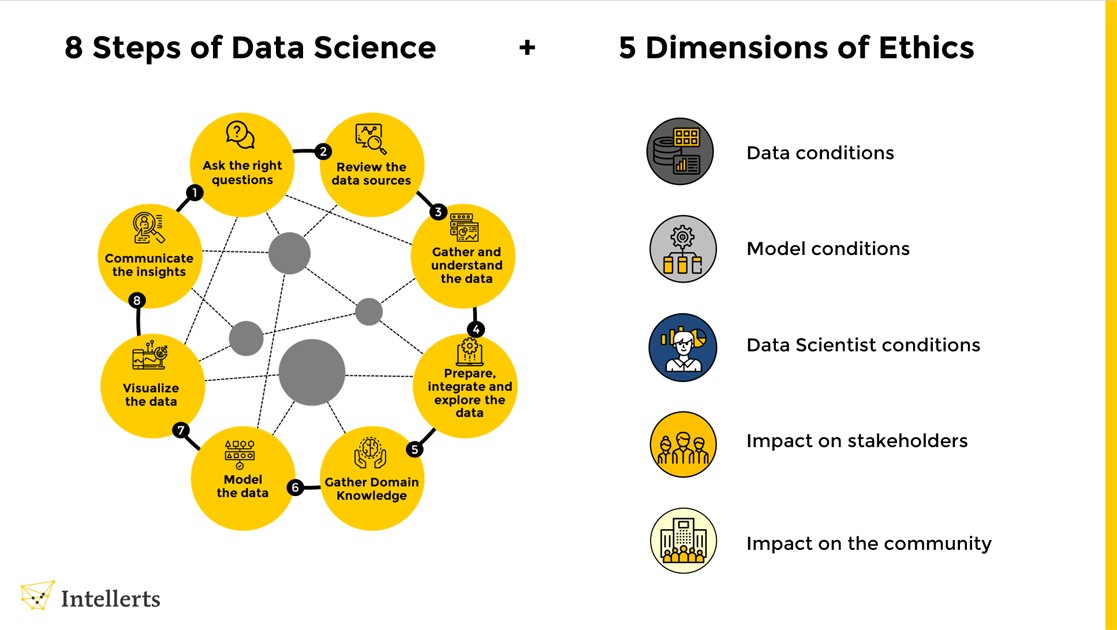
A) Privacy: One of the most critical ethical considerations is privacy. Data scientists must ensure that they are not collecting, storing, or using data that identifies an individual without consent. They should also protect their data from unauthorized access or misuse.
B) Fairness and Bias: Data scientists must ensure fair and unbiased analysis and models. They should be aware of any inherent biases in the data they work with and mitigate them. This includes ensuring that their models are not discriminatory against certain groups or individuals.
C) Transparency: Data scientists should be transparent about their data collection, analysis, and modelling processes. They should clearly communicate their methods, assumptions, and limitations to stakeholders, including their clients, colleagues, and the public.
D) Responsibility: Data scientists should take responsibility for their work’s impact on society. They should consider the potential consequences of their work and mitigate any negative impact.
E) Confidentiality: Data scientists should maintain confidentiality of data they collect or analyse. They should ensure that sensitive information is only accessed by authorized individuals and not shared or sold to third parties without their consent.
F) Professionalism: Data scientists should always act professionally and ethically. They should avoid conflicts of interest and ensure that they do not engage in behaviour that undermines public trust in their profession.
It is our job as data scientists to think critically about algorithmic design and communicate how algorithms work to non-experts. When in doubt ask the stakeholders of the models to weigh in. We call this situated data science where the goal is not to design for but to design with remember to stay kind stay curious and stay critical. In conclusion, data science ethics is a complex and multifaceted issue that requires careful consideration and attention. Data scientists should adhere to ethical principles that promote privacy, fairness, transparency, responsibility, confidentiality, and professionalism. By doing so, they can ensure that they are using data for the greater good and making a positive impact on society.


 There are a few different types of text-to-image generators. One of them is using diffusion models.Diffusion models are trained on a large dataset of hundreds of millions of images.
A word describes each image so the model can learn the relationship between text and images. It is observed that during this training process, the model also knows other conceptual information, such as what kind of elements would make the image more clear and sharp.
After the model is trained, the models learn to take a text prompt provided by the user, create an LR(low-resolution) image, and then gradually add new details to turn it into a complete image. The same process is repeated until the HR(high-resolution) image is produced.
Green dragon on table
Diffusion models don’t just modify the existing images; they generate everything from scratch without referencing any images available online. It means that if you ask them to generate an image of a “dragon on the table,” they would not find an image of the dragon and table individually on the internet and then process further to put the dragon on the table instead of that they will create the image entirely from scratch based on their understanding of the texts during the training time.
There are a few different types of text-to-image generators. One of them is using diffusion models.Diffusion models are trained on a large dataset of hundreds of millions of images.
A word describes each image so the model can learn the relationship between text and images. It is observed that during this training process, the model also knows other conceptual information, such as what kind of elements would make the image more clear and sharp.
After the model is trained, the models learn to take a text prompt provided by the user, create an LR(low-resolution) image, and then gradually add new details to turn it into a complete image. The same process is repeated until the HR(high-resolution) image is produced.
Green dragon on table
Diffusion models don’t just modify the existing images; they generate everything from scratch without referencing any images available online. It means that if you ask them to generate an image of a “dragon on the table,” they would not find an image of the dragon and table individually on the internet and then process further to put the dragon on the table instead of that they will create the image entirely from scratch based on their understanding of the texts during the training time.  Sloth in pink water
There are many benefits of using diffusion models over other models. Firstly, these are more efficient to train. The images generated by them are more realistic and connected to the world. Also, it makes it easier to control the generated image, you can just use the color of the dragon(let’s say green dragon) in the text prompt, and the models will generate the image.
Sloth in pink water
There are many benefits of using diffusion models over other models. Firstly, these are more efficient to train. The images generated by them are more realistic and connected to the world. Also, it makes it easier to control the generated image, you can just use the color of the dragon(let’s say green dragon) in the text prompt, and the models will generate the image.