Artificial Intelligence Archives - CUTTING EDGE VISIONARIES

Ethics Of Data Science

April 24, 2023 by Ankush Mishrain Artificial Intelligence, Machine learningLeave a Comment

Reading Time: 3 minutes

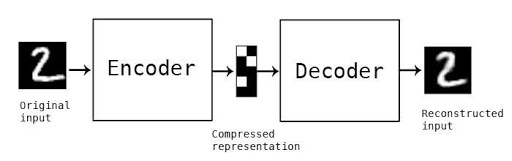
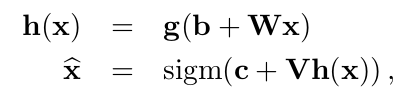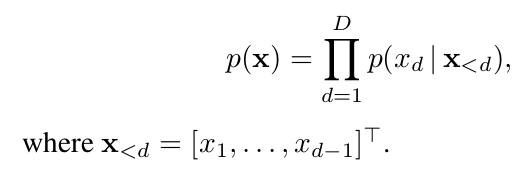With great power comes great responsibility. These are the words of Stan Lee author of the Spider-Man comic book series but where does data power arise from and what are the responsibilities for us as data scientists? First let’s talk about power. In May 2017 the Economist ran the following headline “The world’s most valuable resource is no longer oil but data in fact”. The data as the replacement oil analogy originated from 2006 when Clive Humbly from Tesco in the UK said data is the replacement oil. It’s valuable, but unrefined, it’s useless, and that’s where you come in.

Being a data scientist is a powerful and privileged role; you have highly sought after skills, skills that most people cannot learn. So, you may be granted respect, authority and power simply for being a data scientist. Let’s talk about responsibility. When you think of data science you might think of business models like those that optimize ad revenue. Even these seemingly trivial data science tasks come with a lot of responsibility. A small mistake could lead to a lot of money lost for your company. Data science is used in every field imaginable from marketing to medicine and from transportation to waste management. While a data scientist might feel a bit removed from the real-world implementations of their work their models and analytics will eventually affect real-life decisions. As such, data scientists must adhere to ethical principles when handling data. Data science ethics involves principles, guidelines, and standards that guide data use responsibly and fairly. Data scientists have access to an immense amount of data, and they should use it judiciously and responsibly. The following are some ethical considerations for data scientists.

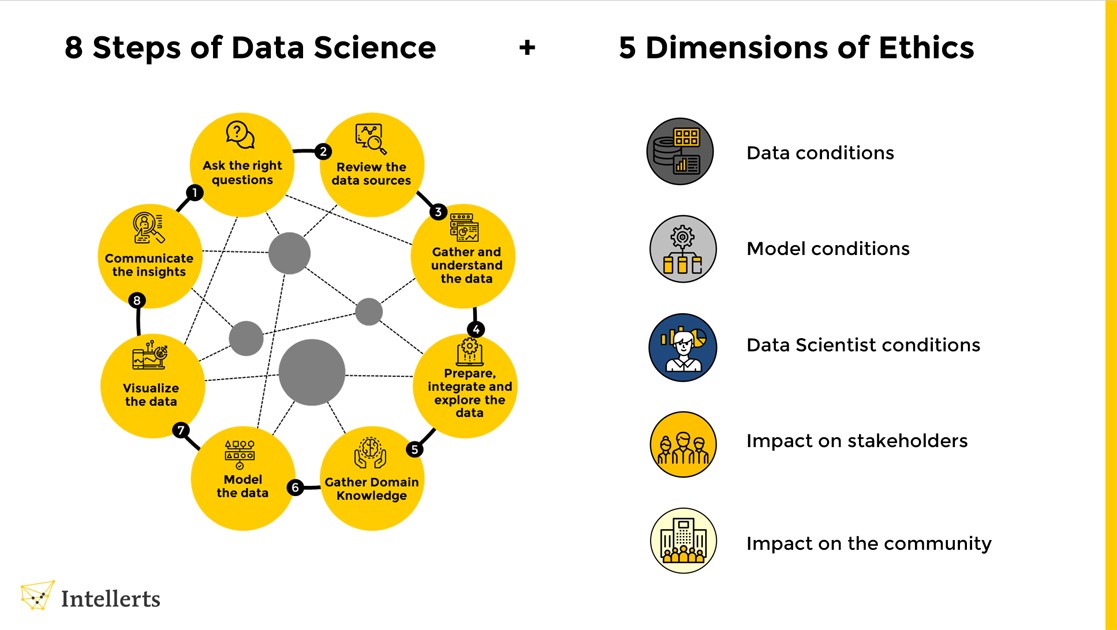
A) Privacy: One of the most critical ethical considerations is privacy. Data scientists must ensure that they are not collecting, storing, or using data that identifies an individual without consent. They should also protect their data from unauthorized access or misuse.

B) Fairness and Bias: Data scientists must ensure fair and unbiased analysis and models. They should be aware of any inherent biases in the data they work with and mitigate them. This includes ensuring that their models are not discriminatory against certain groups or individuals.

C) Transparency: Data scientists should be transparent about their data collection, analysis, and modelling processes. They should clearly communicate their methods, assumptions, and limitations to stakeholders, including their clients, colleagues, and the public.

D) Responsibility: Data scientists should take responsibility for their work’s impact on society. They should consider the potential consequences of their work and mitigate any negative impact.

E) Confidentiality: Data scientists should maintain confidentiality of data they collect or analyse. They should ensure that sensitive information is only accessed by authorized individuals and not shared or sold to third parties without their consent.

F) Professionalism: Data scientists should always act professionally and ethically. They should avoid conflicts of interest and ensure that they do not engage in behaviour that undermines public trust in their profession.

It is our job as data scientists to think critically about algorithmic design and communicate how algorithms work to non-experts. When in doubt ask the stakeholders of the models to weigh in. We call this situated data science where the goal is not to design for but to design with remember to stay kind stay curious and stay critical. In conclusion, data science ethics is a complex and multifaceted issue that requires careful consideration and attention. Data scientists should adhere to ethical principles that promote privacy, fairness, transparency, responsibility, confidentiality, and professionalism. By doing so, they can ensure that they are using data for the greater good and making a positive impact on society.

AI GENERATING IMAGINATIVE PICTURES

April 12, 2023April 12, 2023 by KHUSHI SOLANKIin Art, Artificial Intelligence, Machine learningLeave a Comment

Reading Time: 3 minutes

You must have heard about AI generating many artworks, especially images; ever wondered how this works? In this blog, We will brief you about AI-generated pictures and how they are generated and processed further. AI is the abbreviation of Artificial Intelligence. It refers to a computer that is capable of mimicking human intelligence. This can be done by training an AI system on a large dataset using some algorithms. So artificial intelligence is trained on a large dataset to generate the described image by the user. AI images can be realistic or abstract and convey a specific theme or message. An AI text-to-image generator uses a machine learning technique known as a neural network which can take text as input and generate an image as output. To do this, a neural network requires a lot of training. We can understand this by taking an analogy of a toddler learning for the first time to paint and then making a connection between the painting, objects, and words. To generate images, the system uses two neural networks. The first neural network is used to create the image based on the text input by the user. The second neural network analyzes the generated image with reference images. By comparing the photos, it creates a score to determine the accuracy of the generated image.

There are a few different types of text-to-image generators. One of them is using diffusion models.Diffusion models are trained on a large dataset of hundreds of millions of images. A word describes each image so the model can learn the relationship between text and images. It is observed that during this training process, the model also knows other conceptual information, such as what kind of elements would make the image more clear and sharp. After the model is trained, the models learn to take a text prompt provided by the user, create an LR(low-resolution) image, and then gradually add new details to turn it into a complete image. The same process is repeated until the HR(high-resolution) image is produced. Green dragon on table Diffusion models don’t just modify the existing images; they generate everything from scratch without referencing any images available online. It means that if you ask them to generate an image of a “dragon on the table,” they would not find an image of the dragon and table individually on the internet and then process further to put the dragon on the table instead of that they will create the image entirely from scratch based on their understanding of the texts during the training time.

Sloth in pink water There are many benefits of using diffusion models over other models. Firstly, these are more efficient to train. The images generated by them are more realistic and connected to the world. Also, it makes it easier to control the generated image, you can just use the color of the dragon(let’s say green dragon) in the text prompt, and the models will generate the image.

MADE: Masked Autoencoder for Distribution Estimation

September 10, 2020September 10, 2020 by Dushyant Trivedi. IIT Kharagpurin Machine learningLeave a Comment

Reading Time: 8 minutes

These days, everyone is talking about GANs like BigGAN and StyleGAN, and their remarkable and diverse results on massive image datasets. Yeah, the results are pretty cool! However, this has led to a decline in the research of other generative models like Autoregressive models and Variational Autoencoders. So today, we are going to understand one of these unnoticed generative models: MADE.

Generative models are a big part of deep unsupervised learning. They are of two types—Explicit models, in which we can explicitly define the form of the data distribution, and Implicit models, in which we cannot explicitly define the density of data. MADE is an example of a tractable density estimation model in explicit models. Its aim is to estimate a distribution from a set of examples.

The model masks the autoencoder’s parameters to impose autoregressive constraints: each input can only be reconstructed from previous inputs in a given ordering. Autoencoder outputs can be interpreted as a set of conditional probabilities, and their product, the full joint probability.

Autoregression is a time series model that uses observations from previous time steps as input to a regression equation to predict the value at the next time-step.

Autoencoders

Autoencoder is an unsupervised neural network that learns how to compress and encode data efficiently then learns how to reconstruct the data back from the reduced encoded representation to a representation that is as close to the original input as possible.

Autoencoder for MNIST

The process of transforming input x to latent representation z is called the encoder and from latent variable z to reconstructed version of the input is referenced as the decoder.

Lower dimensional latent representation has lesser noise than input and contains essential information of the input image. So the information can be used to generate an image that is different from the input image but within the input data distribution. By computing dimensionally reduced latent representation z, we are ensuring that the model is not reconstructing the same input image.

Now we want to impose some property on autoencoders, such that its output can be used to obtain valid probabilities. By using autoregressive property, we can transform the traditional autoencoder approach into a fully probabilistic model.

Let’s suppose we are given a training set of examples .Here and , because we are concentrating on binary inputs. Our motivation is to learn a latent representation, by which we can obtain the distribution of these training examples using deep neural networks.

Suppose the model contains one hidden layer and tries to learn h(x) from its input x such that from it, we can generate reconstruction which is as close as possible to x. Such that,

Where W and V are matrices, b and c are vectors, g is a non-linear activation function and sigm is a sigmoid function.

Cross-entropy loss of above autoencoder is,

We can treat as the model’s probability that is 1, so l(x) can be understood as a negative log-likelihood function. Now the autoencoder can be trained using a gradient descent optimization algorithm to get optimal parameters (W, V, b, c) and to estimate data distribution. But the loss function isn’t actually a proper log-likelihood function. The implied data distribution isn’t normalized . So outputs of the autoencoder can not be used to estimate density.

Distribution Estimation as Autoregression

We can write joint probability as a product of their conditional probabilities by chain rule,

Define, and . So now the loss function in the previous part becomes a valid negative log-likelihood function.

Here each output must be a function taking as input only and giving output the probability of observing value at the dimension. Computing above NLL is equivalent to sequentially predicting each dimension of input x, so we are referring to this property as an autoregressive property.

Masked Autoencoders

Since output must depend on the preceding inputs , it means that there must be no computational path between output unit and any of the input units

So we want to discard the connection between these units by element-wise multiplying each weight matrix by a binary mask matrix, whose entries that are set to ‘0’ correspond to the connections we wish to remove.

Where MW and MV are mask matrices of the same dimension as W and V respectively, now we want to design these masks in a way such that they satisfy the autoregressive property.

To impose the autoregressive property, we first assign each unit in the hidden layer an integer m between 1 and D-1 inclusively. The kth hidden unit’s number m(k) represents the maximum number of input units to which it can be connected. Here values 0 and D are excluded because m(k)=0 means it is a constant hidden unit, and m(k)=D means it can be connected to maximum D input units, so both the conditions violate the autoregressive property.

There are few things to notice in the above figure,

Input 3 is not connected to any hidden unit because no output node shouldn’t depend on it.
Output 1 is not connected to any previous hidden unit, and it is estimated from only the bias node.
If you trace back from output to input units, you can clearly see that autoregressive property is maintained.

Let’s consider Multi-layer perceptron with L hidden layers,

For every layer, ml(k) stands for the maximum number of connected inputs of the kth unit in the lth layer. In above figure, value written in each node of MADE architecture represents ml(k).

The constraints on the maximum number of inputs to each hidden unit are encoded in the matrix masking the connections between the input and hidden units:

And these constraints are encoded on output mask matrix:

Where , and. Note that ≥ becomes > in output mask matrix. This thing is vital as we need to shift the connections by one. The first output x2 must not be connected to any nodes as it is not conditioned by any inputs.

We set ml(k) for every layer by sampling from a discrete uniform distribution defined on integers from mink’ ml-1(k’) to D-1 whereas m0 is obtained by randomly permuting the ordered vector [1,2,…,D].

MV,W = MVMW1MW2…MWL represents the connectivity between inputs and outputs. Thus to demonstrate the autoregressive property, we need to show that MV,W is strictly lower diagonal, i.e. MV,Wd’,d is 0 if d'<=d.

Let’s look at an algorithm to implement MADE:

Pseudocode of MADE

Deep NADE models require D feed-forward passes through the network to evaluate the probability p(x) of a D-dimensional test vector, but MADE only requires one pass through the autoencoder.

Inference

Essentially, the paper was written to estimate the distribution of the input data. The inference wasn’t explicitly mentioned in the paper. It turns out it’s quite easy, but a bit slow. The main idea (for binary data) is as follows:

Randomly generate vector x, set i=1
Feed x into autoencoder and generate outputs for the network, set p = .
Sample from a Bernoulli distribution with parameter p, set input xi = Bernoulli(p).
Increment i and repeat steps 2-4 until i > D.

The inference in MADE is very slow, it isn’t an issue at training because we know all x<d to predict the probability at dth dimension. But at inference, we have to predict them one by one, without any parallelization

Left: Samples from a 2 hidden layer MADE. Right: Nearest neighbour in binarized MNIST.

Though MADE can generate recognizable 28X28X1 images on MNIST dataset, it is computationally expensive to generate high dimensional images from a large dataset.

Conclusion

MADE is a straightforward yet efficient approach to estimate probability distribution from a single pass through an autoencoder. It is not capable of generating comparably good images as that of state-of-the-art techniques (GANs), but it has built a very strong base for tractable density estimation models such as PixelRNN/PixelCNN and Wavenet. Nowadays, Autoregressive models are not used in the generation of images and it is one of the less explored areas in generative models. Nevertheless, its simplicity makes room for the advancement of research in this field.

Automation in Medical Science

February 17, 2020February 17, 2020 by Shivansh, Rakeshin Artificial IntelligenceLeave a Comment

Reading Time: 3 minutes

Applied Machine Learning in Healthcare

Google’s machine learning algorithm to detect breast cancer :

Machine learning in medicine has recently made headlines. Google has developed a machine learning algorithm to help identify cancerous tumors on mammograms. Google is using the power of computer-based reasoning to detect breast cancer, training the tool to look for cell patterns in slides of tissue, much the same way that the brain of a doctor might work. New findings show that this approach — enlisting machine learning, predictive analytics and pattern recognition — has achieved 89 percent accuracy, beyond the 73 percent score of a human pathologist.

Stanford’s deep learning algorithm to detect skin cancer :

Stanford is using a deep learning algorithm to identify skin cancer. They made a database of nearly 130,000 skin disease images and trained their algorithm to visually diagnose potential cancer. From the very first test, it performed with inspiring accuracy. Although this algorithm currently exists on a computer, the team would like to make it smartphone compatible in the near future, bringing reliable skin cancer diagnoses to our fingertips.

Robot Assisted Surgery

Robot-assisted surgery became a viable option in 2000, when the Da Vinci Surgical System — a minimally invasive robotic surgeon that is capable of performing complex surgeries — was approved by the FDA. Since then, over 1.75 million robotic surgery procedures have been performed, with “better visualization, increased precision, and enhanced dexterity compared to laparoscopy” according to the NIH. The Da Vinci system average cost is between $1.5M and $2M, which makes it quite unaffordable for small and medium sized hospitals.

It’s not replacement; It’s Displacement

While it’s understandable that doctors are concerned about medical automation — the reality is that machines will not replace doctors; they will just displace them. Patients will always need the human touch, and the caring and compassionate relationship with the people who deliver care.

There’s One Thing : No Machine Can Do Better Than a Doctor

Machines can only learn from precedent; they cannot ideate new ways of diagnosing, they cannot identify new diseases, and they cannot hypothesize new treatment methods. Because of this, the role of the doctor in our society will always be privileged, and will never disappear.

One serious problem is that of expectation of what AI can really do. At the end of the day, an AI system is educated and trained to solve a particular problem and that is pretty much its entire universe.

These systems are not humans, who can freely interact with their environment.

They are machines, not people. The question is no longer whether AI will fundamentally change the workplace. It’s happening.

The true question is how companies can successfully use AI in ways that enables, not replaces, the human workforce, helping to make humans faster, more efficient and more productive.

Data drives all the algorithms on which the automated machines work

As more data is available, we have better information to provide patients. Predictive algorithms and machine learning can give us a better predictive model of mortality that doctors can use to educate patients. But machine learning needs a certain amount of data to generate an effective algorithm. Much of machine learning will initially come from organizations with big datasets. Health Catalyst is developing Collective Analytics for Excellence (CAFÉ™), an application built on a national de-identified repository of healthcare data from enterprise data warehouses (EDWs) and third-party data sources.

Human touch

Many patients feel that being touched is important to getting better

Compassion can reduce pain after surgery, improve survival rates and boost the immune system. …

Patients have significantly better outcomes when their physicians score high on empathy.

Endoscopy-Bot

An endoscopy is a procedure where a small camera or tool on a long wire is shoved into the body through a “natural opening” to a search for damage, foreign objects, or traces of disease.

Even more impressive are so called “capsule endoscopies” where the procedure is boiled down to the simple act of swallowing a pill-sized robot that travels along your digestive tract gathering data and taking pictures that can be sent directly to a processor for diagnostics.

DEEPMIND ALPHAFOLD: The Next Giant Leap By Humans

January 20, 2019 by Hrishabh Sharmain Artificial IntelligenceLeave a Comment

Reading Time: 3 minutesIt has nearly taken hundreds of centuries to get where we are today. From the invention of the wheel to the fastest train with speed of 603 Kmph, from the discovery of fire to landing on the moon, all the technological advances that you use in everyday life, unnoticed, is the result of enthusiastic effort and genius of the great legacy. Artificial intelligence is certainly is the next giant step in that series, the rate of technological advancement would be ever high! Following the one such initiative:

DeepMind is the world leader in artificial intelligence research and its application for positive impact on the world.
DeepMind was founded in London and backed by some of the most successful technology entrepreneurs in the world and have been acquired by Google in 2014.
DeepMind, an AI lab is the complete outsider to the field of molecular biology, beat top pharmaceutical companies like Novartis, Pfizer, etc. at predicting protein structures.
DeepMind has brought together experts from fields if structural biology, physics, machine learning to apply cutting edge techniques to predict the 3D structure of a protein based on its genetic sequence.
DeepMind Alpha Fold is the system which uses vast genomic data to predict protein structure.
CASP (Critical assessment of structure prediction) is a virtual protein folding Olympics, where the aim is to predict the 3D structure of the protein based on its genetic sequence data.
DeepMind has won the CASP13 protein folding competition.
Alpha Fold scores 127.99 was 20 points higher than the second-ranked team, achieving what CASP called “unprecedented progress in the ability of computational methods to predict protein structure”.

What is protein folding problem?

Proteins are our bodies building blocks and perform a vast array of essential functions.

A protein molecule is made of a string of smaller components called amino acids, which fold into the molecule’s 3D shape. The protein folding problem involves determining how the string of amino acids encodes the 3D shape of a protein molecule. This can produce a better understanding of proteins and enable scientists to change their function for the good of our bodies. For example in treating diseases caused by misfolded proteins, such as Alzheimer’s, Parkinson’s, Huntington’s and cystic fibrosis.

The protein folding problem is regarded as one of the grandest biochemistry challenges of the last 50 years. Current approaches include using algorithms to compute the 3D structure of proteins with amino acids sequence data, or using X-ray crystallography and other techniques to image a protein structure.

The DeepMind’s approach:

DeepMind researchers used deep neural network to learn the correlation between the shape of a protein molecule and its amino acid sequence.
The physical properties of a protein molecule include the distance between pairs of amino acids and the angles between chemical bonds that connect those amino acids.

The model came up with a score that estimates the accuracy of a proposed protein structure, then used gradient descent a common deep learning algorithm that finds the minimum of a function to optimize that score.
DeepMind has been working on protein folding for two years and has significantly advanced the development of protein engineering.

Thanks for reading.

BY- AJAY KUMAR RACHURI (3rd year EC )

CHEERS, TEAM CEV.