On the occasion of auspicious Diwali, team CEV wonders what could be more relevant and important other than to talk about harmonic resonance!!
Haha, but no kidding!
Since Diwali is a festival of “lights” and in these days harmonics are unanimously voted as the most popular villain in electrical world to turn the “lights” out!
Well if you have been a new reader at CEV, we would like to bring into your notice that our CEV’s Aantarak division have been literally obsessed with power harmonics for a long time now. We had carried out in-depth preliminary literature recon followed by collaborative effort to develop our own harmonic analyzer from scratch. Both can be accessed by following links respectively:
Pollution in Power Systems;
Continuing the same lines, we walked another mile to get ourselves around the harmonic resonance phenomenon, which otherwise has been tagged as seriously spurious.
We really hope to wind up our intuition for harmonics and related phenomenon in this last blog of the series, so we wish to describe it in its full glory. So, you might encounter some repeating themes, apologies for that.
The Crisp
For any domain, having a glance of history really helps in getting a larger picture of the things. Being aware of the historical background greatly aids in understanding the things with continuity and help in extrapolating the ongoings to get some future insights.
So EE folks haven’t begun struggling with harmonics in recent times, infact one can trace it back to early 20th century when power systems were in its earliest phase. Charles Proteus Steinmetz, yes the same engineer who taught the world how to draw the equivalent circuit diagram of induction motor and gave us a handy notation of “j” to simplify our AC calculations had made an excellent introductory paper in harmonics. At that time due to inferior core materials transformers and motors saturated, giving rise to these problems. However, now the problems- harmonics pose remain unchanged but the sources and impact have been magnified manifold.
21st-century power system seems to be literally littered with inky-dinky semiconductor devices which draws currents which are severely offbeat from sinusoidal nature, moreover, the advent of high power electronics has made the situation more vulnerable. Technically these devices/loads are called Non-linear devices/loads, and problem they pose are quite spurious in nature. We know that high-frequency components of these currents called harmonics interact with power system in ways leading to overheating of components, flickering, circuit breaker false trippings, or even causing catastrophic events like a wide-area power outage (aka. Blackouts), as reported by many utilities in recent times across the world.
These harmonics can tune the capacitor banks used for power factor improvement and voltage stability in resonance with the power system components and lead to blowing up of the banks and causing further contingencies, like voltage collapse, etc.
In this blog, a detailed analysis of power factor banks, non-linear loads, resonance phenomenon in RLC, and lastly the resonance in power system due to harmonics is carried out.
One more note, you might be aware of the MATLAB company tagline, it reads “accelerating the pace of science and engineering”, and CEV is really goanna help MATLAB do that here. We will use appropriate MATLAB simulation models to verify the theory and bring home to the readers a sophisticated understanding of the phenomenon.
The Skyrocketing hopes!!!
The flow
Power Factor Capacitor Banks
Thevenin’s Equivalent of Power System
Electrical Resonance in RLCs
Harmonic Resonance with PF Capacitor Banks
Harmonic Resonance, is among the most dreaded phenomenon the power system harmonics are observed to unroll.
ABB, the mega-giant in the power system industry tries to bring on the table the significance of eliminating power harmonics by its product commercial.
Though being regarded as the most suspected reason for unexplained failures of electric utilities the harmonic resonance is a phenomenon that could be explained in a paragraph of no more than 100 words only, you would be able to do it the small kids around you, by the end.
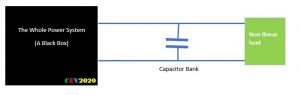
The story begins from the power factor capacitors banks……
You might have appreciated the fact that the use shunt capacitor banks across the electrical motors (lagging loads) can improve the power factor greatly.
The underlying idea is to provide the reactive power locally instead of drawing it from the system thereby reducing the supply current and preventing the elements of the whole power system (from T-lines down to the generators) from overloading.
This concept can be intuitively understood by use of following graphs.
Consider a sinusoidal voltage applied across an inductive load, result is a lagging current.
So, the convention is to simply connect a capacitor bank of required capacitance. Since the capacitor is in parallel so the voltage across it is in phase with load terminal voltage, and the current through it is obviously 90 degrees leading the voltage across it.
The phasor diagram:
The waveforms are like:
Adding the parallel currents to get the supply current:
So, it could be easily seen that the peak of the resultant current has been reduced, at the same time the power factor angle is also reduced hence power factor improved!!
This same result can be concluded by simply adding the current vectors mathematically.
So, what exactly is happening here?
The picture becomes crystal clearer if we try to simulate an RL load with shunt capacitor and visualize the instantaneous power consumed by each element.
By putting appropriate parameter values, it could be seen that when inductor is absorbing power the capacitor is releasing its stored power, and when the inductor is releasing the stored inductive power in its magnetic field, the capacitor is absorbing it in its electric field. It is this inductive and capacitive power, are collectively called reactive power, which just flows in the system but never manifests itself as real power, rather just oscillates. If this power exchange becomes equal then no net reactive power is drawn from the source.
So final result is “significantly reduced net reactive power drawn from the source and so is the supply current”.
Question: Do you think that the capacitor in ceiling fans of households serves the purpose of PF improvement?
Now to analyze the effect of shunt capacitor for non-linear loads, i.e. loads that produce harmonics, we have to follow a different approach, a completely different line of attack.
However, the theory we just saw is equally true, but as far as harmonics are concerned, we are more interested in first understanding the frequency response, rather than power calculation.
Some of the most basic and prevalent techniques used everywhere and all the time in power system analysis are first required to be grasped before we try to understand what happens for non-linear loads.
- The concept of Thevenin’s equivalent;
- The concept of current injecting vector
- The concept of superposition
Thevenin’s Equivalent of Power System
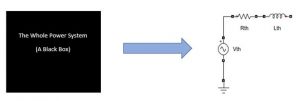
Consider this point of view, the two-terminal is supplying a single-phase non-linear load, also conventionally a power capacitor is applied in parallel to supply reactive power locally. The black box here is an abstraction of all the distribution and transmission transformers, transmission lines and the generators and whatnot, all working in synchronism.
So, the Thevenin theorem says that the black box can be represented by an equivalent emf source and an equivalent impedance in series, called Thevenin’s voltage and Thevenin’s impedance respectively.
- The Thevenin voltage is simply the open circuit terminal voltage.
- And the Thevenin impedance is the impedance seen by the load given all the voltage and current sources are deactivated.
Once the Vth and Zth are known, to know the impact of connecting a load impedance to already loaded grid we don’t go on solving whole vast electric mesh again. A revolutionary French electrical engineer LC Thevenin in 1880s came up with a revolutionary method to enormously simplify the large electrical circuit.
Find Vth and Zth. Now turn off all the sources, connect the load wherever required, excite the point with the negative Vth, find the drop and add the drops algebraically to already existing system. This is applicable only for linear system by virtue of superposition theorem. This line of attack is chosen when the load impedance is center point (i.e. load impedance is known). This is quite a popular technique and is implied to calculate the impact of loading on different buses of system, fault analysis for a known value of fault impedance, etc.
Now, if impact of a given load current is point of attention (rather than the load impedance) then we use slightly different approach. We turn off the source and inject an equal load current at the point of connection of load, find drops at different nodes and again added algebraically to the existing system.
Now in this case of harmonic resonance study, notice we are utterly concerned with the load current. Our prime moto is to see the impact of a given non-sinusoidal load current on the system.
Here it is important to reflect to one important fact. Our power system is built up of thousands of different kinds of elements, the generators synchronous and asynchronous IMs, the transformers, T-lines, cables, a huge variety of loads, yet all of them can be modelled as a combination of just three fundamental elements, resistance, inductance and capacitance.
Q. How would you modify the Thevenin equivalent if the power systems have power electronic components?
So, it is all those little-tiny things learnt in early engineering classes of circuit theory comes back to manifest in harmonic resonance and other complicated higher phenomenon. Here we realise that solving the RLC circuit is not dull, unless we know how far-reaching are the meaning of those Rs, Ls and Cs in a practical applications.
But all of these theories are strictly applicable to a linear system.
Think for a second how to manipulate the tools for the non-linear currents.
So, lets revisit our aim, our aim is to find the impact of non-sinusoids, that means we are trying to see the response of system subjected to different frequencies. Now this leading us to a completely different space. Did you remember a phenomenon related when we check the response of a system to input of different frequencies?
You guessed it right, the series and parallel RESONANCE!!!!!
Moreover, we are finding the frequency response and by the time we have completed the course in control engineering, frequency response characteristics of any system almost become synonymous to bode plot.
It becomes as good as people screaming to you to “draw frequency characteristics” and you literally hear “draw plot bode-plot”!
And why not, after all, bode plot is a plot of the logarithm of magnitude of steady state output to input for different frequency of sinusoidal input excitations.
Electrical Resonance in RLCs
Resonance in series circuit can be identified as a phenomenon in which for a given magnitude of sinusoidal voltage source, current through the branch reaches maximum at some angular frequency of voltage source.
Here is bode-plot for the system considering the voltage signals as input and the current in the branch as output:
Scilab codes: (one can use Matlab too)
s=poly (0, ‘s’); p = s/ (8174.52 +2s +0.03s²); p= syslin (c, ‘p’); clf (); bode (p, 1, 5000)
For R=2, C=120uF, L=30 mH
The plot indicates that at a certain frequency of voltage excitation the current through the circuit reaches its maximum value.
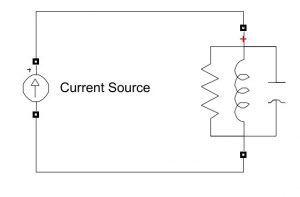
Similarly, parallel resonance can be identified as a phenomenon in which for a given magnitude of sinusoidal current source, the voltage across the branch reaches a maximum at some angular frequency of the current source.
Reflecting on these two base-statement rest all of the conditions of resonance can be deduced.
So here is a bode-plot of parallel RLC circuit taking voltage across the elements as output and total current as input.
In this case the voltage reaches a peak corresponding to the resonant frequency.
Harmonic Resonance with PF Capacitor Banks
We have built all the necessary parts and now it’s the time to put all the parts together to see the larger picture, and really wind-up our intuition around the harmonic resonance. We started with this not so technical diagram:
Reflect back and finally, we have:
It is now quite evident that parallel resonance is seen where parallel elements are excited by a range of angular frequency currents. These parallel elements in a power system are formed by the PF capacitors and the Thevenin’s equivalent at the node. The non-linear load is going to act as a source of different angular frequency current source. So, if the non-linear loads have the harmonic component which has a frequency as the natural frequency of the RLC then a parallel resonance is unavoidable fate.
And this is in-short the hack of harmonic resonance in power systems.
Wouldn’t it be delightful to let a kid know about this?
A Practical Approach
- How to obtain the harmonic spectrum of a non-linear load?
Matlab gives you an elegant way forward, use a spectrum analyzer (in a correct configuration)
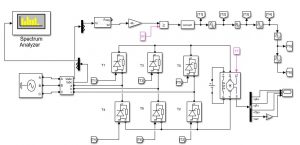
A sample case of a popular non-linear load, a three-phase rectifier:
A severely off-beat source current:
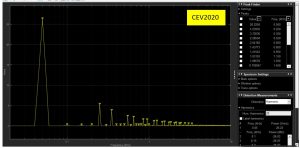
Here is what its harmonic spectrum looks like:
NOTE: 6-Pulse rectifiers have a current THD of 26% and significant harmonics are 5th (250 Hz), 7th (350 Hz) and 11th.
- How to obtain the Thevenin equivalent of a power system?
The answer remains the same the MATLAB provides an elegant way to do it.
Using an impedance measurement block:
What you get is:
If you are observant enough, these plots contain all of the data that we are searching to be able to predict a harmonic resonance in capacitor bank across the non-linear load.
Well, we will leave it to you to build and run the models for yourself because we don’t want to steal your pride of finding and fixing things out on your own, so good-luck…………
However, in the end, we will be kind enough to atleast make a conclusion:
The conclusion reached is, when the non-linear load has a current component of frequency close or equal to the natural frequency, the system goes in parallel resonance i.e. system impedance is highest. For a given current value at the highest impedance would clearly result in the highest voltage drop across the capacitor, hence maximum current through it (notice the value of capacitive reactance decrease at higher frequencies).
The capacitor is immediately blown, as a result, the reactive power is drawn from the supply leading to increased current, thereby blowing the main fuse also. And the last sad thing to be noted is that if the capacitor comes out to be a utility capacitor and non-linear load is quite heavy then a blackout in the area is unavoidable destiny.
What is even more surprising is that current harmonics produce parallel resonance that we just saw, however, if there are harmonics presence in voltage waveform then series resonance could also occur in a dramatic way. Causing the collapse of a perfectly healthy bus due to non-linear load at another bus. One can also work-out its details on our own!
We hope we have inspired you enough to get yourself easy with the extremely useful tools in Electrical engineering, the massive MatLab and the sweet Scilab, and hope that CEV team effort boosts you a step towards your holy dream vision for the world!!
Happy Diwali 2020.
TEAM CEV!!!
Featured Image courtesy pixabay.com.